Chapter 3 Nuclear Magnetic Resonance Perry Sprawls, Ph.D.
Link to Book Table of Contents	Chapter Contents Shown Below

Introduction And Overview  

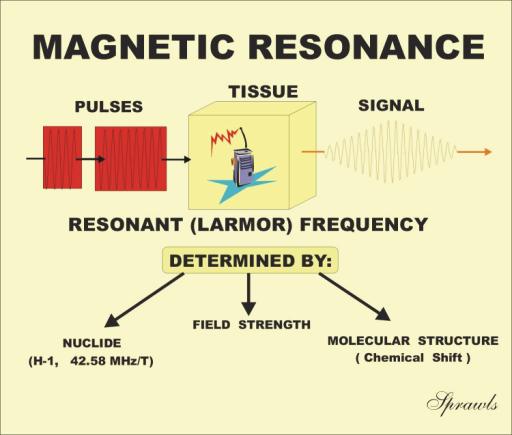
When certain materials, such as tissue, are placed in a strong magnetic field, two things happen. The materials take on a resonant characteristic and they become magnetized. In this chapter we will consider the resonant characteristic. In Chapter 4 we will study the magnetization effect. Resonance means the materials can absorb and then re-radiate RF radiation at a specific frequency, like a radio receiver-transmitter, as illustrated in Figure 3-1. It is actually the nuclei of the atoms that resonate. The phenomenon is generally known as nuclear magnetic resonance (NMR). The resonant frequency of material such as tissue is typically in the RF range so that the emitted radiation is in the form of radio signals. The specific resonant frequency is determined by three factors as shown in the illustration and will be described in detail later. The characteristics of the RF signals emitted by the material are determined by certain physical and chemical characteristics of the material. The RF signals produced by the NMR process can be displayed either in the form of images (MRI) or as a graph depicting chemical composition (MR spectroscopy).

Figure 3-1. The concept of Nuclear Magnetic Resonance (NMR).

Magnetic Nuclei  

Materials that participate in the MR process must contain nuclei with specific magnetic properties. In order to interact with a magnetic field, the nuclei themselves must be small magnets and have a magnetic property or magnetic moment, as shown in Figure 3-2. The magnetic characteristic of an individual nucleus is determined by its neutron-proton composition. Only certain nuclides with an odd number of neutrons and protons are magnetic. Even though most chemical elements have one or more isotopes with magnetic nuclei, the number of magnetic isotopes that might be useful for either imaging or in vivo spectroscopic analysis is somewhat limited. Among the nuclides that are magnetic and can participate in an NMR process, the amount of signal produced by each nuclide varies considerably.

Figure 3-2. Magnetic and non-magnetic nuclei.

 Spins

Protons and neutrons that make up a nucleus have an intrinsic angular momentum or spin. Pairs of protons and neutrons align in such a way that their spins cancel. However, when there is an odd number of protons or neutrons (odd mass numbers), some of the spins will not be canceled and the total nucleus will have a net spin characteristic. It is this spinning characteristic of a particle with an electric charge (the nucleus) that produces a magnetic property known as the magnetic moment.

            It is for this reason that magnetic nuclei, such as protons, are often referred to as spins.

            The magnetic property, or magnetic moment, of a nucleus has a specific direction. In Figure 3-2, the direction of the magnetic moment is indicated by an arrow drawn through the nucleus.

 RF Signal Intensity

 The intensity of the RF signal emitted by tissue is probably the most significant factor in determining image quality and the time required to acquire an image. This important issue is considered in Chapters 10 and 11. We now begin to introduce the factors that contribute to signal intensity.

            During the imaging process, the body section is divided into an array of individual volume elements, or voxels. It is the signal intensity from each voxel that determines image quality. The signal is produced by the magnetic nuclei within each voxel. Therefore, signal intensity is, in general, proportional to the quantity of magnetic nuclei within an individual voxel. We now consider the factors that affect the number of magnetic nuclei within an individual voxel

 Relative Signal Strength

 The relative signal strength from the various chemical elements in tissue is determined by three factors: (1) tissue concentration of the element; (2) isotopic abundance; and (3) sensitivity of the specific nuclide.

            In comparison to all other nuclides, hydrogen produces an extremely strong signal. This results from its high values for each of the three contributing factors.

            Of the three factors, only the concentration, or density, of the nuclei varies from point to point within an imaged section of tissue. The quantity is often referred to as proton density and is the most fundamental tissue characteristic that determines the intensity of the RF signal from an individual voxel, and the resulting pixel brightness. In most imaging situations, pixel brightness is proportional to the density (concentration) of nuclei (protons) in the corresponding voxel, although additional factors, such as relaxation times, modify this relationship.

            Protons in solids, such as the tabletop and bone, do not produce signals. Signals come only from protons in molecules that are free to move, as in a liquid state.

 Tissue Concentration of Elements

 The concentration of chemical elements in tissue covers a considerable range, depending on tissue type and such factors as metabolic or pathologic state. The concentrations of elements in tissue are in two groups. Four elements—hydrogen, carbon, nitrogen, and oxygen—typically make up at least 99% of tissue mass.

            The most abundant isotopes of the four elements are hydrogen-1, carbon-12, nitrogen-14, and oxygen-16. Note that the mass number of hydrogen (1) is odd while the mass numbers of the other three (12, 14, 16) are even. Therefore, hydrogen is the only one of these four isotopes that has a strong magnetic nucleus. The nucleus of the hydrogen-1 atom is a single proton. Among all the chemical elements, hydrogen Spins  is unique in that it occurs in relatively high concentrations in most tissues, and the most abundant isotope (H-1) has a magnetic nucleus.

            Other elements, such as sodium, phosphorus, potassium, and magnesium, are present in very low concentrations. Calcium is concentrated in bone or localized deposits.

            Within this group of elements with low tissue concentrations are several with magnetic nuclei. These include fluorine-19, sodium-23, phosphorus-31, and potassium-39.

 Isotopic Abundance

 Most chemical elements have several isotopes. When a chemical element is found in a naturally occurring substance, such as tissue, most of the element is typically in the form of one isotope, with very low concentrations of the other isotopic forms. For the three elements— carbon, nitrogen, and oxygen—that have a high concentration in tissue, the magnetic isotopes are the ones with a low abundance in the natural state. These include carbon-l3, nitrogen-15, and oxygen-17.

 Relative Sensitivity and Signal Strength

 The signal strength produced by an equal quantity of the various nuclei also varies over a considerable range. This inherent NMR sensitivity is typically expressed relative to hydrogen-1, which produces the strongest signal of all of the nuclides. The relative sensitivities of some magnetic nuclides are shown in Table 3-1.

Table 3-1. Relative Sensitivities of Some Magnetic Nuclides

In summary, hydrogen has a lot going for it: 1) a high tissue concentration; 2) the most abundant isotope (H-1) is magnetic; and 3) it produces a relatively strong signal compared to an equal concentration of other nuclei. That is why hydrogen is the only element that is imaged with conventional MRI systems.

 Radio Frequency Energy

 During an imaging procedure, RF energy is exchanged between the imaging system and the patient’s body. This exchange takes place through a set of coils located relatively close to the patient’s body as we saw in Chapter 2. The RF coils are the antennae that transmit energy to and receive signals from the tissue.

 Pulses

 RF energy is applied to the body in several short pulses during each imaging cycle. The strength of the pulses is described in terms of the angle through which they rotate or flip the magnetic nuclei and the resulting tissue magnetization, as described later. Many imaging methods use both 90˚ and 180˚ pulses in each cycle.

 Signals

 At a specific time in each imaging cycle, the tissue is stimulated to emit an RF signal, which is picked up by the coils, analyzed, and used to form the image. The spin echo or gradient echo methods are generally used to stimulate signal emission. Therefore, the signals from the patient’s body are commonly referred to as echoes.

 Nuclear Magnetic Interactions

The NMR process is a series of interactions involving the magnetic nuclei, a magnetic field, and RF energy pulses and signals.

 Nuclear Alignment

 Recall that a magnetic nucleus is characterized by a magnetic moment. The direction of the magnetic moment is represented by a small arrow passing through the nucleus. If we think of the nucleus as a small conventional magnet, the magnetic moment arrow corresponds to the south pole-north pole direction of the magnet.

            In the absence of a strong magnetic field, magnetic moments of nuclei are randomly oriented in space. Many nuclei in tissue are not in a rigid structure and are free to change direction. In fact, nuclei are constantly tumbling, or changing direction, because of thermal activity within the material; in this case, tissue.

            When a material containing magnetic nuclei is placed in a magnetic field, the nuclei experience a torque that encourages them to align with the direction of the field. In the human body, however, thermal energy agitates the nuclei and keeps most of them from aligning parallel to the magnetic field. The number of nuclei that do align with the magnetic field is proportional to the field strength. The magnetic fields used for imaging can align only a few of every million magnetic nuclei present. However, this is sufficient to produce a useful NMR effect.

 Precession and Resonance

When a spinning magnetic nucleus aligns with a magnetic field, it is not fixed; the nuclear magnetic moment precesses, or oscillates, about the axis of the magnetic field, as shown in Figure 3-3. The precessing motion is a physical phenomenon that results from an interaction between the magnetic field and the spinning momentum of the nucleus.

Figure 3-3. Magnetic nuclei precession and resonance in a magnetic field.

            Precession is often observed with a child’s spinning top. A spinning top does not stand vertical for long, but begins to wobble, or precess. In this case, the precession is caused by an interaction between the earth’s gravitational field and the spinning momentum of the top.

            The precession rate (cycles per second) is directly proportional to the strength of the magnetic field. It is this precessing motion that makes a nucleus sensitive and receptive to incoming RF energy when the RF frequency matches the precession rate. This precession rate corresponds to the resonant frequency. It is the precessing nuclei, typically protons, that are tuned to receive and transmit RF energy.

Excitation

 If a pulse of RF energy with a frequency corresponding to the nuclear precession rate is applied to the material, some of the energy will be absorbed by the individual nuclei. The absorption of energy by a nucleus flips its alignment away from the direction of the magnetic field, as shown in Figure 3-4. This increased energy places the nucleus in an unnatural, or excited, state.

Figure 3-4. The excitation of a magnetic nucleus by the application  of a pulse of RF energy.

            In MRI an RF pulse is used that flips some of the nuclei into the transverse plane of the magnetic field. In this excited state the precession is now transformed into a spinning motion of the nucleus around the axis of the magnetic field. It should be noted that this spinning motion is an enhanced precession and is different from the intrinsic spin of a nucleus about its own axis.

            The significance of a magnetic nucleus spinning around the axis of the magnetic field is that this motion now generates an RF signal as shown in Figure 3-5. It is this signal, from many nuclei, that is collected to form the MR image.

Figure 3-5. RF signal production by magnetic nuclei spinning  in the transverse plane of a magnetic field.

Relaxation

 When a nucleus is in an excited state, it experiences an increased torque from the magnetic field, urging it to realign. The nucleus can return to a position of alignment by transferring its excess energy to other nuclei or the general structure of the material. This process is known as relaxation.

            Relaxation is not instantaneous following an excitation. It cannot occur until the nucleus is able to transfer its excess energy. How quickly the energy transfer takes place depends on the physical characteristics of the tissue. In fact, the nuclear relaxation rate (or time) is, in many cases, the most significant factor in producing contrast among different types of tissue in an image.

We are more interested in the collective relaxation of many nuclei that produce the magnetization of tissue and will return to this point in the next chapter.

 Resonance

The significance of the nuclear precession is that it causes the nucleus to be extremely sensitive, or tuned, to RF energy that has a frequency identical with the precession frequency (rate). This condition is known as resonance and is the basis for all MR procedures. NMR is the process in which a nucleus resonates, or “tunes in,” when it is in a magnetic field.

            Resonance is fundamental to the absorption and emission of energy by many objects and devices. Objects are most effective in exchanging energy at their own resonant frequency. The resonance of an object or device is determined by certain physical characteristics. Let us consider two common examples.

            Radio receivers operate on the principle of resonant frequency. A receiver can select a specific broadcast station because each station transmits a different frequency. Tuning a radio is actually adjusting its resonant frequency. Its receiver is very sensitive to radio signals at its resonant frequency and insensitive to all other frequencies.

            The strings of a musical instrument also have specific resonant frequencies. This is the frequency at which the string vibrates to produce a specific audio frequency, or musical note. The resonant frequency of a string depends on the amount of tension. It can be changed, or tuned, by changing the tension. This is somewhat analogous to the resonant frequency of a magnetic nucleus being dependent on the strength of the magnetic field in which it is located.

 Larmor Frequency

The resonant frequency of a nucleus is determined by a combination of nuclear characteristics and the strength of the magnetic field. The resonant frequency is also known as the Larmor frequency. The specific relationship between resonant frequency and field strength is an inherent characteristic of each nuclide and is generally designated the gyromagnetic ratio. The Larmor frequencies [in megahertz (MHz)] for selected nuclides in a magnetic field of 1 T are shown in Table 3-2.

Table 3-2. Larmor Frequencies for Selected Nuclides in a Magnetic Field

 The fact that different nuclides have different resonant frequencies means that most MR procedures can “look at” only one chemical element (nuclide) at a time.

 Field Strength

 For all nuclides, the resonant frequency is proportional to the strength of the magnetic field. In a very general sense, increasing the magnetic field strength increases the tension on the nuclei (as with the strings of a musical instrument) and increases the resonant frequency. The fact that a specific nuclide can be tuned to different radio frequencies by varying the field strength (i.e., applying gradients) is used in the imaging process.

 Chemical Shift

 The resonant frequency of magnetic nuclei, such as protons, is also affected by the structure of the molecule in which they are located.

            When a proton, or other magnetic nucleus, is part of a molecule, it is slightly shielded from the large magnetic field. The amount of shielding depends on the chemical composition of the molecule. This means that protons in different chemical compounds will be in slightly different field strengths and will therefore resonate at different frequencies. This change in resonant frequency from one compound to another is known as chemical shift. It can be used to perform chemical analysis in the technique of MR spectroscopy and to produce images based on chemical composition. However, in conventional MRI the chemical-shift effect can be the source of an unwanted artifact.

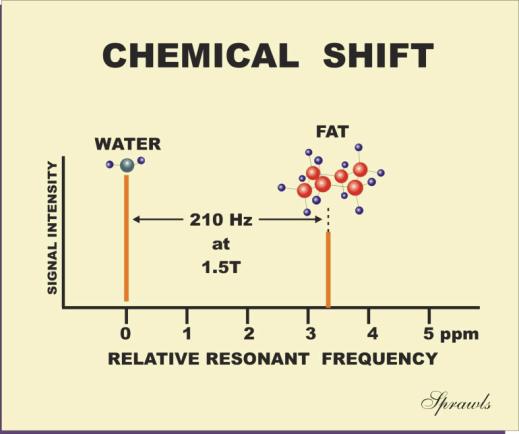
            In tissue the chemical shift in resonant frequency between the fat and water is approximately 3.3 ppm, as shown in Figure 3-6. At a field strength of 1.5 T the protons have a basic resonant frequency of approximately 64 MHz. Multiplying this by 3.3 gives a water-fat chemical shift of approximately 210 Hz. At a field strength of 0.5 T the chemical shift would be only 70 Hz.

Figure 3-6. The chemical shift effect on the relative resonant frequency  of protons in fat and water.

            There are several imaging techniques that can be used to selectively image either the water or fat tissue components. One approach is to suppress either the fat or water signal with specially designed RF pulses. This technique is known as spectral presaturation and will be described in Chapter 8. Another technique makes use of the fact that the signals from water and fat are not always in step, or in phase, with each other and can be separated to create either water or fat images.

Mind Map Summary

Nuclear Magnetic Resonance

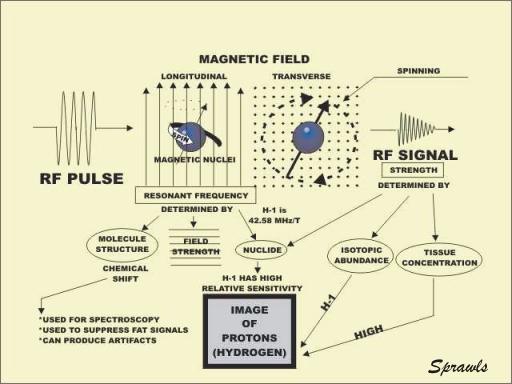
            When a magnetic nucleus is located in a strong magnetic field, it resonates. In effect, it becomes a tuned radio receiver and transmitter. The resonance occurs because the spinning nucleus precesses at a rate that is in the radio frequency range. The resonant frequency is determined by three factors. Each specific nuclide has a unique resonant frequency. The resonant frequency is affected to a small degree by the structure of the molecule containing the magnetic nucleus. This, the chemical shift effect, is useful for spectroscopy and to suppress fat signals in images. It can also lead to a certain type of image artifact. The resonant frequency is directly proportional to the strength of the magnetic field. This is useful because it makes it possible to tune the various parts of a body to different frequencies by applying magnetic field gradients.

            When an RF pulse is applied to a magnetic nucleus oriented in the longitudinal direction, it can be flipped into the transverse plane. There the nucleus spins around the axis of the magnetic field and generates an RF signal. It is the signals from many spinning nuclei that are collected and used to form the image. It is necessary to have strong signals to produce good images. Signal strength depends on three factors. Each magnetic nuclide has a unique sensitivity or relative signal strength. All chemical elements have several different isotopes, but all isotopes of an element are usually not in the form of magnetic nuclei. Therefore, the abundance of the magnetic isotope for a specific element has a major effect on signal strength. To produce strong signals a tissue must have a relatively high concentration of a chemical element and the most abundant isotope of that element must be magnetic.

            Hydrogen is the only chemical element with a high concentration in tissue and body fluids in the form of an isotope that has a magnetic nucleus. Therefore, MR imaging is essentially limited to visualizing only one chemical element, hydrogen.